4753. Кинотеатр+
Однажды, ученики
B-й школы города G решили съездить в кино. Администрация кинотеатра расположила
их в зале размера n × m, который специально был подобран так,
чтобы все места были заняты школьниками. Каждому посетителю кинотеатра был выдан
свой номер.
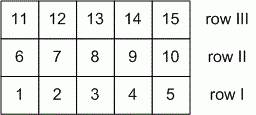
Школьники заняли
свои места следующим образом: они входили в зал в порядке, в котором шли их
номера, и полностью занимали сначала первый ряд, потом второй, потом третий и
т.д.
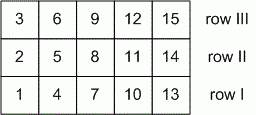
Однако классный
руководитель решил, что такая рассадка плохо влияет на поведение учащихся и
пересадил их по-другому: ученики сначала занимали все первые места каждого
ряда, потом все вторые места каждого ряда и т.д. (см. рисунок).
Администрация
решила выяснить, сколько учащихся не поменяют своего места после пересадки.
Вход. В первой строке
заданы числа n и m (1 ≤ n, m ≤ 109).
Выход. Выведите одно
число – количество учеников, которые в результате пересадки остануться сидеть
на тех же местах.
|
Пример
входа 1 |
Пример
выхода 1 |
|
3 4 |
2 |
|
|
|
|
Пример
входа 2 |
Пример
выхода 2 |
|
3 3 |
3 |
РЕШЕНИЕ
массив
Анализ алгоритма
Заполним два двумерных массива как сказано в условии задачи
(0 ≤ i < n, 0 ≤ j < m):
·
массив c1 заполним как сели школьники: c1[i][j]
= i * m + j + 1;
·
массив c2 заполним как пересадил школьников классный
руководитель: c2[i][j] = j
* n + i + 1;
Приравняем c1[i][j]
и c2[i][j]:
i * m + j + 1 = j * n + i
+ 1,
i * (m – 1) = j * (n
– 1), i / j = (n – 1) / (m – 1) = p / q,
где p / q – несократимая
дробь. Отсюда
 , 0 ≤ l ≤ min((n – 1) / p, (m – 1) / q)
, 0 ≤ l ≤ min((n – 1) / p, (m – 1) / q)
Пусть d = НОД(n – 1, m – 1), тогда  или
или  .
.
Следовательно 0 ≤ l ≤ min((n – 1) / p, (m – 1) / q) = min(d, d) = d.
Количество
таких l, для которых существует пара (i, j) = (pl, ql) что c1[i][j]
= c2[i][j], равно d + 1.
Пример
Пусть размеры
кинотеатра равны n = 19, m = 7.
Тогда d = НОД(n – 1, m – 1) = НОД(18, 6) = 6. Дробь p / q равна 18 / 6 = 3 / 1 (p = 3, q = 1). Парами (i, j), для которых c1[i][j] = c2[i][j] или i * m + j + 1 = j * n + i
+ 1, будут (pl, ql) = (3l, l), где 0 ≤ l ≤ 6:
|
l = 0: (i, j) = (0, 0); |
l = 4: (i, j) = (12, 4); |
|
l = 1: (i, j) = (3, 1); |
l = 5: (i, j) = (15, 5); |
|
l = 2: (i, j) = (6, 2); |
l = 6: (i, j) = (18, 6); |
|
l = 3: (i, j) = (9, 3); |
|
Реализация алгоритма
Читаем входные данные.
scanf("%lld %lld",&n,&m);
Вычисляем и выводим ответ, равный НОД(n – 1, m – 1) + 1.
d =
gcd(n-1,m-1);
printf("%lld\n",d+1);